Scientist of the Day - Roger Joseph Boscovich

Portrait of Ruđer Josip Bošković, by Robert Edge Pine, 1760, location unknown (Wikimedia commons)

Ruđer Josip Bošković, a Croatian-Italian Jesuit natural philosopher, was born May 18, 1711, in Ragusa (now Dubrovnik), Croatia.  He was educated at the Jesuit seminary in Ragusa, excelled in his academic work, and was soon sent to Italy, where he spent the bulk of his career, teaching mathematics at the Collegio Romano in Rome, and in Milan. The name he (and we) began with is Croatian; to Italian Jesuits, he was known as Ruggiero Giuseppe Boscovich, and to the English, he was Roger Joseph Boscovich.

Title page of Theoria philosophiae naturalis, by Ruđer Josip Bošković, 1763 (Linda Hall Library)

Boscovich is often described as a polymath, which he was not, if you require that your polymaths be proficient in many different and unrelated disciplines.  Boscovich did important work in geometry, optics, astronomy, geodesy, and even engineering, but they all fall under the heading of the mathematical sciences, and as far as I know, he made no contributions to natural history, geology, medicine, or anatomy.  So Aristotle, Gottfried Wilhelm von Leibniz, Alexander von Helmont, and Thomas Young were legitimate polymaths – Boscovich was not.  But in the fields that he chose, he was brilliant.  He helped measure the length of a degree of the meridian in Italy, figured out how to determine the orbit of a comet from just three observations, designed three-lens eyepieces for telescopes, invented a tool to measure the dispersion of glass, and would have had many similar and notable accomplishments on his resume, had he made a resume.  These were set forth in a slew of books, 12 of which we have here in our Library.

First plate, showing atomic forces in figure 1, engraving in Theoria philosophiae naturalis, by Ruđer Josip Bošković, 1763 (Linda Hall Library)

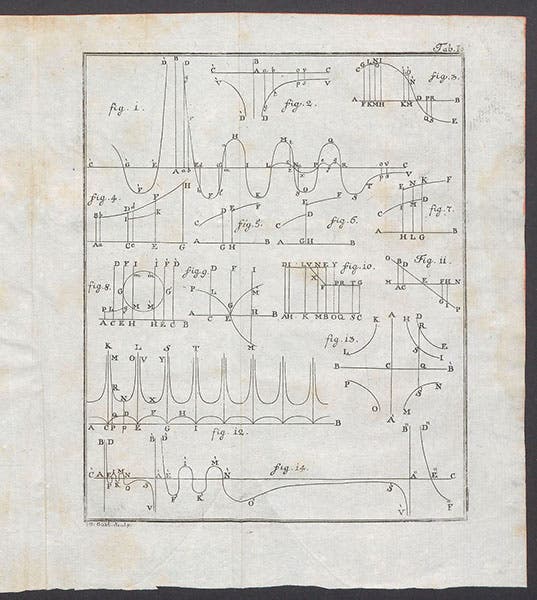
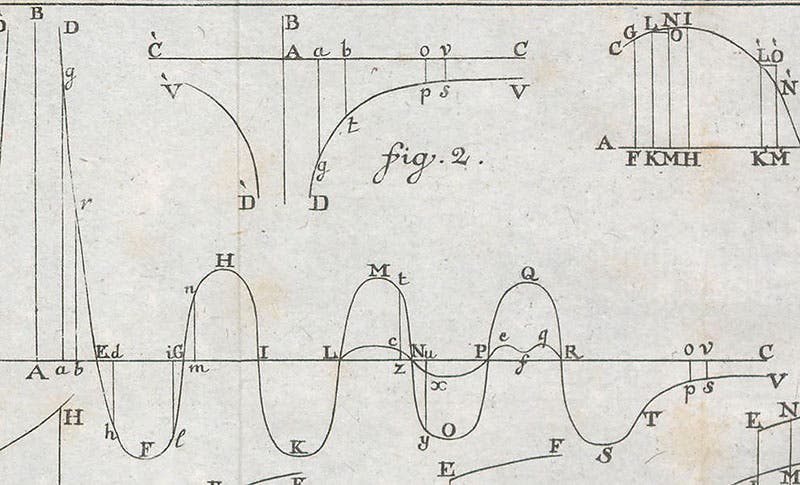
But today, we are going to discuss just one of his books, Theoria philosophiae naturalis (A Theory of Natural Philosophy), published originally in Vienna in 1758 in an edition now quite scarce, and then republished in Venice in 1763, which is the edition most often cited, and the one we have in our Library.  In this work, Boscovich proposed a theory of the atom that has been called the "point theory".  He argued that Newton's theory of hard, impenetrable, indivisible, but elastic atoms was impossible in Nature, as there is no way to explain how one atom could collide with and rebound from another without it stopping and reversing in an infinitesimally small amount of time, which would result in its going in two directions at once.  He proposed instead that an atom is a dimensionless point, with no extension in space at all, surrounded by forces that alternately attract and repel other atoms.  In a daunting plate of geometrical diagrams (third image), his scheme showing the attraction and repulsion of a point atom is figure 1 at the top, which we enlarge in our fourth image.  A point atom is at A, and the squiggly line that weaves from D through H, M, and Q to V is the attractive force (if below the X axis) or the repulsive force (if above the X axis) felt by another atom.  Since the repulsion at D is on the way to becoming infinite, this explains why two atoms never actually hit each other before rebounding.  Boscovich found that he could explain most physical and chemical behavior with his point atoms.

Figure 1, detail of third image, showing the attractive and repulsive forces surrounding a point atom, engraving in Theoria philosophiae naturalis, by Ruđer Josip Bošković, 1763 (Linda Hall Library)

Now the reason why I trouble you with these abstruse details is that Boscovich came very close to defining what would later be called a "field."  Indeed, I had to work very hard not to use the word “field” in the paragraph above.  In 1844, Michael Faraday first used an electromagnetic field to explain certain phenomena, and James Clerk Maxwell soon took the matter up in his famous equations that define electrical and magnetic fields.  Did Faraday get the idea from Boscovich?  When I was in graduate school, the answer was an emphatic Yes.  In his Michael Faraday: A Biography (1965), L. Pearce Williams spent 8 pages discussing Boscovich’s point-atoms and subsequently maintained that Faraday drew on Boscovich for his field theory.  Unfortunately, more recent scholarship has downplayed the importance of Boscovich for Faraday.  In his very readable Michael Faraday: A Very Short Introduction (2010), Frank A.J.L. James emphatically rejects a Boscovich connection and prefers other social and religious factors for shaping Faraday’s world view.  In three other recent semi-popular biographies of Faraday that I consulted out of curiosity, Boscovich’s name does not appear anywhere.

Statue of Ruđer Josip Bošković in Milan, using the Italian form of his name, Ruggiero Giuseppe Boscovich (Wikimedia commons)

But if Boscovich was not the father of field theory in practice, he certainly deserves credit for introducing the idea of point atoms and force fields 80 years before other physicists found their way to those concepts. He was the last great Jesuit scientist, before the Jesuit order was disbanded by decree of the Pope in 1773.  Fortunately, the order was later restored, and Jesuits would return to the scientific forefront in the century after Boscovich.  

Wooden model of the Observatory at Brera, perhaps built by Boscovich himself, Museo Nazionale Scienza e Tecnologia Leonardo da Vinci, Milan (Wikimedia commons)

The portrait of Boscovich that everyone uses (first image) is not very well documented, but it is attributed to Robert Edge Pine in London in 1760, and there was such a portrait painter, and Boscovich was in London in 1760, so it seems legitimate, but I have no idea where the painting is now.  There is a statue of Boscovich in Milan, where he designed and founded the Jesuit Observatory at Brera (fifth image).  The Museo Nazionale Scienza e Tecnologia Leonardo da Vinci in Milan has a wooden model of the Observatory at Brera that they think was made by Boscovich, or at least according to his plans (sixth image).  If Boscovich did indeed make it himself, then the claims for “polymathy” for Boscovich become a little stronger.

William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.