Scientist of the Day - Pythagoras of Samos
Imagined portrait of Pythagoras of Samos, engraving in The History of Philosophy, by Thomas Stanley, 1687 (Linda Hall Library)
Pythagoras, an early Greek social reformer, religious thinker, and possible mathematician, was born on the island of Samos, just off the coast of Ionia, sometime around 570 BCE. We know very little about him, except that he left Samos at the age of 40 or so and moved to the Greek colony of Croton in what was then Magna Graecia, and is now the boot of Italy. He founded a religious brotherhood, bound to secrecy, and taught metempsychosis, the migration of souls after death, to his followers. The brotherhood also adhered to strict dietary rules. The Pythagoreans, as they were called, later came to advocate the importance of number and mathematics, and Pythagoras himself may have introduced those ideas, but we really don’t know. Most scholars of Pythagoras seem to feel that at least some of the passion that Pythagoreans had for numbers and harmony must have come down from the great man himself.
Pythagoras, as envisioned by Raphael Sanzio in his School of Athens, ca 1511, Stanza della Segnatura, Vatican (wga.hu)
The Pythagoreans, and perhaps Pythagoras, were significant in the history of Greek natural philosophy for introducing number and proportion into discussions of the natural world. They are said to have discovered that musical harmonies are determined by number, such that two vibrating strings whose lengths are in the ratio 2/1 will produce a musical octave, and, in similar fashion, 3/2 determines a fifth, and 4/3 a fourth. Plato and Aristotle both attribute this discovery to the Pythagoreans.
Diagram and proof of the Pythagorean theorem, bottom woodcut, Elementa geometria, by Euclid, 1482 (Linda Hall Library)
Pythagoras also, according to some sources, applied those same musical ratios to the movements of the planets, so that their motions produce some kind of intelligible harmony. This would later be called the “harmony of the spheres,” a term not appropriate for the time of Pythagoras, when no one thought in terms of heavenly spheres. But it would become a very popular conceit in Western thought.
The harmonies of the planets, engraved diagram in Harnonices mundi, by Johannes Kepler, 1619 (Linda Hall Library)
Most people think of the Pythagorean theorem when they hear the name Pythagoras. We show you the first diagram of the theorem in a printed book, a Euclid of 1482 (third image). There is no evidence that Pythagoras discovered this. But it does appear that early Pythagoreans did discover (and prove) that the diagonal of a square is “incommensurate” with the sides of the square, another way of saying it cannot be expressed as a ratio, and hence is irrational.
Monochord displaying the harmonies of the spheres, engraving, Utriusque cosmi maioris, by Robert Fludd, 1618 (Linda Hall Library)
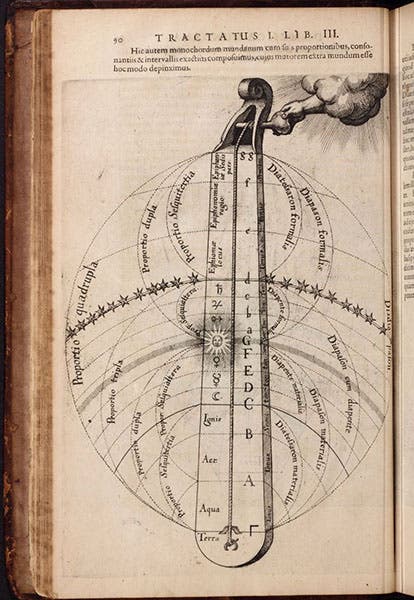
Whatever Pythagoras did or not do himself, there is no doubt this his “ism” – Pythagoreanism – had a powerful influence on Renaissance and early modern science and mathematics, with its emphasis on searching for numbers when describing the world. Raphael included Pythagoras, diagraming harmonies, in the foreground of his fresco, The School of Athens (ca 1511) in the Vatican (third image; for more on this mural, see our post on Raphael). Johannes Kepler was driven by his quest to uncover the true harmonies of the spheres, and in his Harmonices mundi of 1619, he provided us with a remarkable diagram (fourth image), in which he translated the changing speeds of the planets into musical phrases, which do indeed, in his opinion, play out a cosmic symphony. And Robert Fludd left us a memorable diagram of his vision of the Pythagorean notion of the harmony of the spheres (fifth image).
Engraved title page, with Pythagorean vignette at bottom (see detail, next image), Musurgia universalis, by Athanasius Kircher, 1650 (Linda Hall Library)
One of the many stories told about Pythagoras was that he discovered the numerical basis of musical harmony by listening to some blacksmiths pound anvils with their hammers, producing, in some cases, harmonic chords. When the hammers were weighed, it was found that those hammers whose weights were in the ratios of small numbers (4/3, 3/2) produced harmonious sounds. This is certainly not a true story, since weights are not like strings, producing harmonies when their weights are in simple ratios. But it is an enduring one, and Athanasius Kircher, in his encyclopedia on music of 1650, translated the story into a vignette that appeared at the bottom of the engraved title page of his book (sixth and seventh images). Note the diagram of the Pythagorean theorem at the left of the detail (last image).
Scene showing Pythagoras at left, listening to the musical consonances and dissonances produced by blacksmiths’ hammers of different weights, detail of sixth image, engraved title page, Musurgia universalis, by Athanasius Kircher, 1650 (Linda Hall Library)
Since we know hardly anything about the historic Pythagoras, it will not surprise you to learn that we have no authentic portrait. There is a bust in the Capitoline Museum in Rome that is described as a Roman copy of a Greek bust made around the 1st century BCE (i.e., 400 years after Pythagoras), which you can see at this link. I like the re-imagined portrait that we have in our copy of Thomas Stanley’s The History of Philosophy (1687), which we used as our first image.
Finally, there is the coolest of all images of the Pythagorean theorem on the title page of the colored Euclid published by Oliver Byrne in 1835. You may see it as the first image in our post on Byrne.
This is our tenth and last post on Presocratic natural philosophy, so we thought we would add a guide with links to all of the previous posts: Thales of Miletus, Anaximenes of Miletus, Anaximander of Miletus, Heraclitus of Ephesus, Parmenides of Elea, Zeno of Elea, Anaxagoras of Clazomenae, Empedocles, Democritus of Abdera. Next, we will slowly address, as opportunity allows, the Golden Age of Greek natural philosophy: Socrates, Plato, and Aristotle, before moving on to the Alexandrians: Euclid, Eratosthenes, and Archimedes.
William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.
