Scientist of the Day - Hugo Steinhaus

Contents of the rear pocket of Mathematical Snapshots, by Hugo Steinhaus, 1938 (Linda Hall Library)
Hugo Steinhaus, a Polish mathematician and composer of mathematical puzzles, died Feb. 25, 1972, at the age of 85. Six weeks ago, on Jan. 12, 2025, Steinhaus’s birthday, we wrote our first post on Steinhaus, discussing primarily his wonderful puzzle book, Mathematical Snapshots, which went through several English editions, of which the second and third are commonly held, but the first edition (1938) is scarce. I concluded by mentioning that I had located a copy of the elusive first edition, but could not afford to buy it; a photo supplied by the dealer (which I showed) was tantalizing.

Title page, Mathematical Snapshots, by Hugo Steinhaus, 1938 (Linda Hall Library)
We write a second post so soon because Jason Dean, curator of rare books at the library, acquired the copy of the first edition offered for sale, and it has been added to our history of science collections. I wanted to write about it while Steinhaus is still fresh in our minds, because it is a real treat of a book. It is a little jaded on the outside, and if it ever had a dust jacket, it has wandered away. But otherwise, it is just wonderful. Here’s why.

Printed color diagrams illustrating the “knight’s walk” and Euler’s problem of the “36 soldiers,” Mathematical Snapshots, by Hugo Steinhaus, p. 14, 1938 (Linda Hall Library)
The second and third editions have lots of illustrations, but they are ordinary half-tone, black-and white images, devoid of color. Not only does the first edition have illustrations in color, but they are still vibrant, 87 years later. Compare the image for the problem of the “36 soldiers” in the second edition (fourth image) with that in the first (third image). The problem was this: can you arrange 36 officers from 6 different regiments and of 6 different ranks in 6 rows and columns so that only one of each rank and regiment is represented in each row and column? The problem cannot be solved for 36 officers, but can for 25, which is what the diagram at the bottom depicts. I don’t know how the color was applied, or how it could be applied at all, given that the book was printed in Poland, one year before that country was invaded by Hitler.

Uncolored diagrams illustrating the “knight’s walk” and Euler’s problem of the “36 soldiers”, in the second edition of Mathematical Snapshots, by Hugo Steinhaus, p. 21, 1950 (author’s copy)
On another page, Steinhaus explains how to measure the length of an irregular river on a map, using a piece of graph paper. And there, lying loose between the leaves, is a piece of transparent parchment graph paper, evidently supplied by the printer. How it has stayed in place for the past 87 years is a mystery (fifth image).
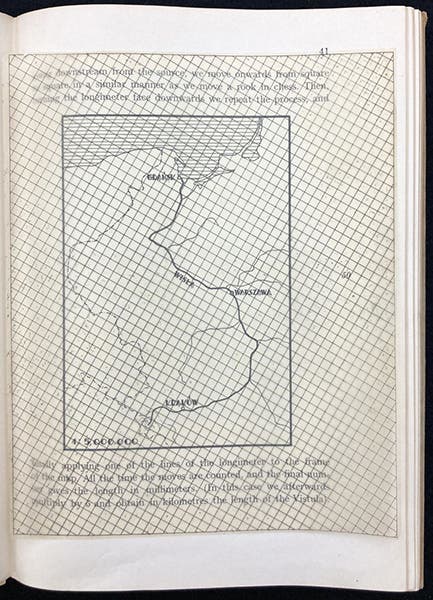
Diagram showing how to measure the length of an irregular river using graph paper, with provided transparent graph paper still in place, Mathematical Snapshots, by Hugo Steinhaus, p. 41, 1938 (Linda Hall Library)
The first edition has 15 3-D geometrical illustrations. They are called anaglyphs, and are printed in red and green (sixth image). To the naked eye, the diagrams are blurry and unclear. Evidently, one needs red-green 3-D glasses to focus the images. Fortunately, you need only search in the pocket at the back to find such glasses (first and last images). The anaglyphs were converted to ordinary illustrations in all later editions. You can also find, in the pocket, two flat halves of a dodecahedron (a 12-sided regular solid made up of pentagons), which, with the help of a rubber-band, can be formed into a 3-D shape, as explained in the text. Each pentagon is printed in one of four colors, none of which touch in the completed dodecahedron, illustrating another theorem discussed in the text (first image).
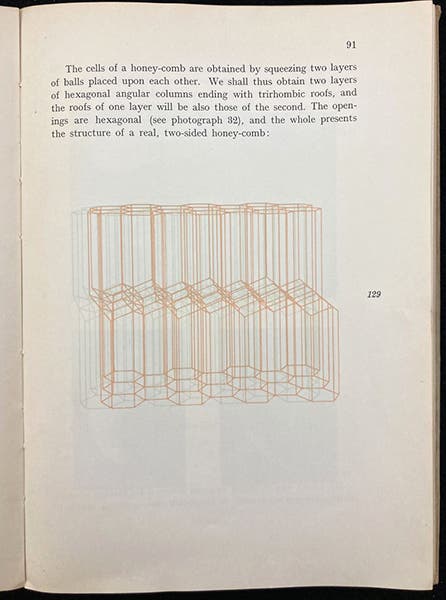
Anaglyph of a geometrical diagram, printed in red and green, to be viewed with 3-D glasses, Mathematical Snapshots, by Hugo Steinhaus, p. 91, 1938 (Linda Hall Library)
Also in the pocket is a deck of 31 tiny, printed cards (first image). If they are in the proper numbered order (as ours are now), you can fan them slowly, and they show a moving point tracing out a cycloid, and three other such sequences, if you fan while holding the other edge, and then turn the deck over and fan again. How amazing is it that all those cards are still in the pocket, after such a passage of time!

Pocket at the end of Mathematical Snapshots, by Hugo Steinhaus, 1938, with contents spilling out (Linda Hall Library)
So we are pleased with our new acquisition. We now have a small collection of fine art books with a science theme, thanks to Jason, and the Mathematical Snapshots of 1938 fits right in, and shows what a clever author and a talented printer can do to enhance a text with color and ingenious added material.
William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.






