Scientist of the Day - Hugo Steinhaus

Mathematicians at the Lwów School of Mathematics, photograph, 1929; Hugo Steinhaus is seated at far left, Bhāvanā magazine, vol, 8 (4), Oct. 2024 (bhavana.org.in)

Hugo Steinhaus, a Polish mathematician and poser of mathematical problems and puzzles, was born Jan. 14, 1887, in Jaslo, a city in southeast Poland that was then part of Austria-Hungary.  His parents were of Jewish heritage; his father was a brick manufacturer. Steinhaus developed an early interest in math, teaching himself for the most part, and ended up studying in Göttingen, one of the European hotbeds for mathematicians, presided over by the great David Hilbert.

Polish math students at Göttingen, group photograph, 1907; Hugo Steinhaus is standing at far right, 20 years of age (Wikimedia commons)

With his PhD in hand, after the interruption of the First World War, Steinhaus joined the faculty of the University of Lwów, now part of Ukraine, but during the period between the two wars, the second most active intellectual and cultural center in Poland (after Warsaw). The University’s School of Mathematics brimmed with mathematicians who would make their mark, many you have never heard of, such as he brilliant Stefan Banach, but also including some whose names you probably recognize, such as Stanislaw Ulam and John von Neumann (not a professor at Llów but a frequent visitor), both of whom came to the United States from Lwów before the Nazi invasion.

Building in Lwów, Poland (now Lviv, Ukraine) that housed the Scottish Café, where the Lwów School of Mathematics met informally and kept the Scottish Book; the café is still there, but it is now part of a hotel (Wikimedia commons).

Steinhaus was one of the grand old men of the department at Lwów (mathematicians peak early), and a founder of an informal mathematical club that met at the Scottish Café in Lwów.  Mostly, they devised problems for each other to solve, and beginning in 1935, they started writing the problems down in a marbled-paper-covered notebook. This continued until May of 1941, and the notebook survived long enough for Elam to make a copy of it at Los Alamos, but its whereabouts now seems to be a secret. Steinhaus was the author of many of the 200+ problems, and he penciled in the last problem in the notebook, before they folded up shop and scattered for the duration of the War.

Dust jacket, Mathematical Snapshots, by Hugo Steinhaus, 3rd Amer. ed., Oxford Univ. Press, 1969 (author’s copy)

I cannot appreciate, much less discuss, Steinhaus’s achievements as a professional mathematician. But I can talk about his prowess as a deviser of mathematical puzzles and problems. I began reading Scientific American in high school, about the time that Martin Gardiner began contributing a “Mathematical Games” column to the magazine every month.  He continued to do so until 1980, a span of almost 25 years, and I not only read and worked through every column, I bought (and still have) all the book compilations of his columns that were published. 

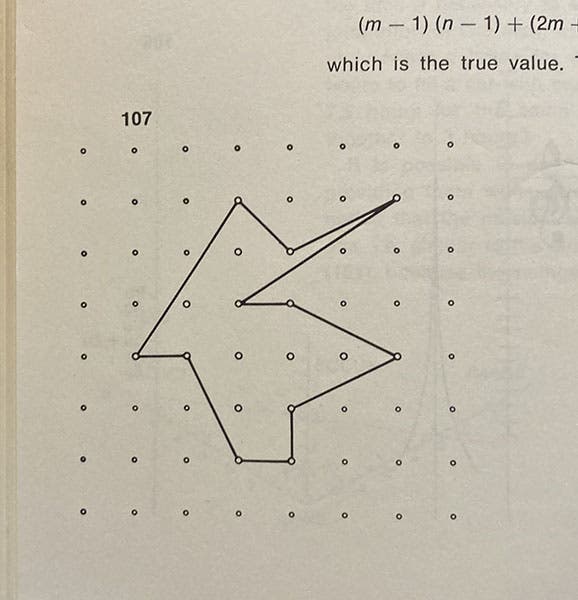
Diagram of Pick’s theorem, Mathematical Snapshots, by Hugo Steinhaus, p. 96, fig. 107, 1969 (author’s copy)

I took an interest in other books of math puzzles and games, and one day I ran across a copy of Mathematical Snapshots, by “H. Steinhaus” (Oxford Univ. Pr., 1969, 3rd Amer. ed.), of whom I had never heard (fourth image).  This collection was totally unlike any of Martin Gardner’s books. There were no proofs or solutions, just a walk-through of the mathematical landscape, with random discussions of mathematical oddities, most of which seemed unbelievable.  For example, on one page (96; fifth image), Steinhaus showed a lattice of points, and then blithely stated that if you construct a polygon, as convoluted as you want, with every vertex on a point of the lattice, then the area of the polygon is equal to the number of lattice points within the polygon, plus one-half the number of lattice points making up the vertices, minus 1.  In the case of the polygon shown, that would be 6 + 11/2 – 1, or 10.5 square units.  That still seems amazing to me, that the shape of the polygon is almost incidental. I later learned that this is known as Pick’s theorem, and is well known to mathematicians. But I had never encountered its like in a book intended for the mathematical puzzler.

Dust jacket, Mathematical Snapshots, by Hugo Steinhaus, 2nd ed., Oxford Univ. Press, 1950 (author’s copy)

I eventually found and bought the second edition of Mathematical Snapshots (1950; sixth image), and, not long ago, went searching for the legendary first edition of 1938, printed in Poland, where many of the figures were anaglyphs – overlapping, out of focus, red-and-green images that were pulled into 3-D by the red-and-green glasses that were thoughtfully included in a pocket at the back of the book. I recently found a copy for sale in Wales, but could not afford it; I hope the bookseller does not mind my showing you the photo he sent me of the goodie-laden pocket (seventh image).  I really should have bitten the bullet and acquired that copy.  I can’t imagine that there are many around with an intact rear pocket.

Rear pocket with red/green glasses and pop-up polygons, Mathematical Snapshots, by Hugo Steinhaus, 1938, Literary Cat Books, Wales (dealer’s copy)

Steinhaus moved to Wrocław after WWII, and brought their math department to a level of eminence equal to that of Lwów between the Wars, He died there on Feb. 25, 1972.

Portrait of Hugo Steinhaus, undated photograph, Bhāvanā magazine, vol, 8 (4), Oct. 2024 (bhavana.org.in)

William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.