Scientist of the Day - Edouard Roche

Édouard Albert Roche, a French mathematician and astronomer, was born Oct. 17, 1820.   He was born in Montpellier, studied at the University of Montpellier, taught there for 34 years, and died in Montpellier in 1883.   He worked in the field of celestial mechanics, which required considerable mathematical dexterity, which Roche apparently possessed in abundance.  And in the field of eponymity, he was an unusual triple-threat, contributing his name to the Roche limit, the Roche sphere, and the Roche lobe.  We will touch on each of these as best we can.

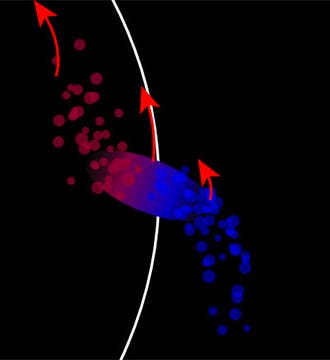
The Roche limit is applicable to any two mutually orbiting bodies, such as the Earth and the Moon. The Roche limit is the minimum distance that the Moon (or any satellite held together only by gravity) can be from the Earth (or any large body) without breaking up. If the Moon comes any closer than the Roche limit, it will break apart because of tidal forces. Thus no planet can have a moon that lies within the Roche limit – it can have only rings. The size of the Roche limit depends on the mass of the two bodies.  For the Earth-Moon system, the Roche limit is about 6000 miles, center to center. So if you were to push the Moon towards the Earth, as it approached the Roche limit it would gradually deform into a potato-shape, and when it reached the Roche limit, it would no longer be able to hold itself together, and it would break apart like instant potato flakes, spreading out slowly into a ring. Of course, while this was happening, people on the Earth would be experiencing tides that were thousands of feet high and could care less that the Moon was falling apart.

Diagram showing the same planet outside the Sun’s Roche limit (white arc) (Wikimedia commons)

Diagram showing a planet deforming as it is brought closer to the Roche limit (white arc) (Wikimedia commons)

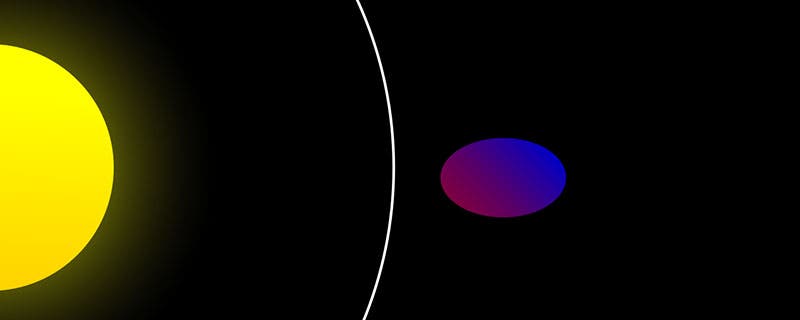
The diagrams here are for a sun and a close-orbiting planet, showing the planet breaking apart at the Roche limit (first image), with a spherical shape well outside the Rohe limit (second image), and deforming when brought near the Roche limit (third image).

Because the Roche limit lies so close to the Earth, it has not affected our relationship to the Moon.  But in the case of very massive planets, it does come into play, and the reason why Saturn has a ring and not a moon at that location is a direct result of Saturn’s Roche limit, as Roche himself pointed out.

The Roche spheres of the Sun (yellow) and the Earth. L1 – L5 are the Lagrange points where the gravitational forces of the two bodies are neutralized (Wikimedia commons)

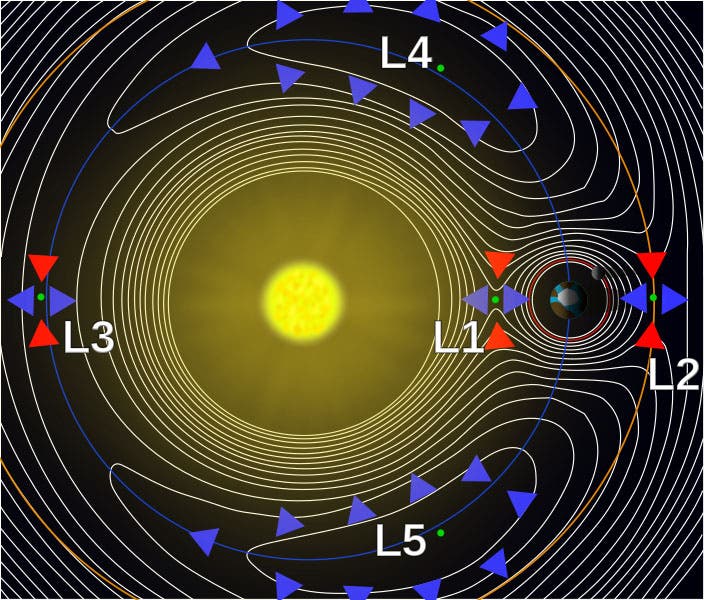
The Roche sphere also applies to two-body systems, such as the Earth and the Moon, or the Sun and the Earth; we will illustrate and discuss the latter (fourth image).  The Sun’s Roche sphere is the region where the Sun’s gravitational sphere predominates.  Outside the Roche sphere, the Earth's gravitational field takes over.  The point where the two gravitational pulls just balance is called a Lagrange point; there are 5 of them for the Sun-Earth system, and they were identified some 80 years before Roche, by Joseph-Louis Lagrange, a former Scientist of the Day. The Roche sphere, incidentally, is now often referred to as the Hill sphere, an unusual case of one eponym usurping another.  William George Hill was an American astronomer; we will have to devote a post to him some day, to see if he merits the eponymic transfer.

Diagram of a binary star system, showing the Roche lobes of a red giant star (left) and a white dwarf (slideplayer.com)

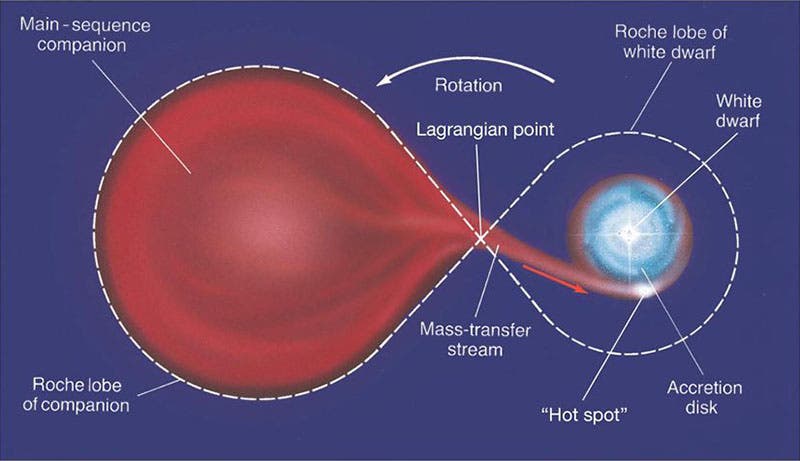
The Roche lobe comes into play when the two orbiting bodies are gaseous, as with a binary star. If the stars are close enough, gas will be pulled from each star toward the other, and the tear-shaped envelope of gas is the Roche lobe (fifth image).

Portrait of Edouard Roche, photograph, 1850s (academie-sciences.fr)

Nearly all of Roche’s work in celestial mechanics was published in the Mémoires of the Academy of Sciences of Montpellier, a publication that is oddly lacking from our serials collection.  So all we have to show here, other than the modern diagrams, is a portrait of Roche (sixth image), taken we would guess in the 1850s.

Dr. William B. Ashworth, Jr., Consultant for the History of Science, Linda Hall Library and Associate Professor emeritus, Department of History, University of Missouri-Kansas City. Comments or corrections are welcome; please direct to ashworthw@umkc.edu.